The Winning Game
Grey overlay
Pink
Green
Blue
Cream
Liliac
Purple
Yellow
Objectives
Developing the Information Technology learning strands, specifically:
- Understands and can apply payoff matrix in evaluating outcomes
- Understands and be able to explain Nash equilibium
- Understands and be able to explain dominant strategy
Nash Equilibrium and Dominant Strategy
Recap - Zero-sum game and Pay-off matrix
- A game is called
zero-sumif the sum of payoffs equals zero for any outcome. That means that the winnings of the winning players are paid by the losses of the losing players. EXAMPLEs of a zero-sum games include poker, rock-paper-scissors and tennis. - Game theory attempts to determine mathematically and logically the actions that “players” should take to secure the best outcomes for themselves in a wide array of “games.”
- A
Payoff matrixis a table used to illustrate the player moves and the outcomes with each possible moves.
Learn It - Payoff matrix in real life example
- Considering two toy companies, A and B. Their profits depending on their decisions on advertising or not.
- The
payoff matrixof their decisions is as following:

Learn It: Nash Equilibrium
- Suppose two cars are driving towards a junction from perpendicular directions
- The light is green for one and red for the other
- If the police would not ticket the drivers, would they want to break the law?
- To help you understand this scenario and possible outcomes, lets watch a short 4 minutes video:
A Nash Equilibriumis a law that no one would want to break even in the absence of external force such as police in the traffic light example or in the ice cream example- Formally,
Nash Equilibriumis a state where no players can improve their outcomes by change of strategy as long as others remain unchanged.
Badge It Silver
create a payoff matrix for the following scenario:
- Two cars are meeting at an intersection and want to proceed as indicated by the arrows in Figure shown below.
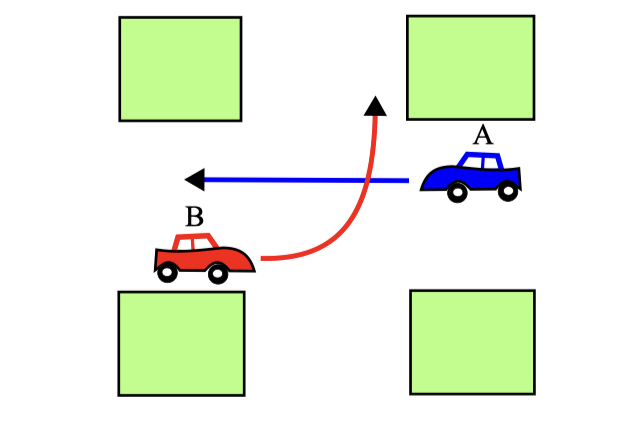
- Each player can proceed or move. If both proceed, there is an accident. A would have a payoff of -100 in this case, and B a payoff of -1000 (since B would be made responsible for the accident, since A has the right of way). If one yields and the other proceeds, the one yielding has a payoff of -5, and the other one of +5. If both yield, it takes a little longer until they can proceed, so both have a payoff of -10.
- Analyze this simultaneous game, draw the payoff bimatrix
- Two cars are meeting at an intersection and want to proceed as indicated by the arrows in Figure shown below.
Badge It Gold - Prisoners' dilemma and Nash equilibrium
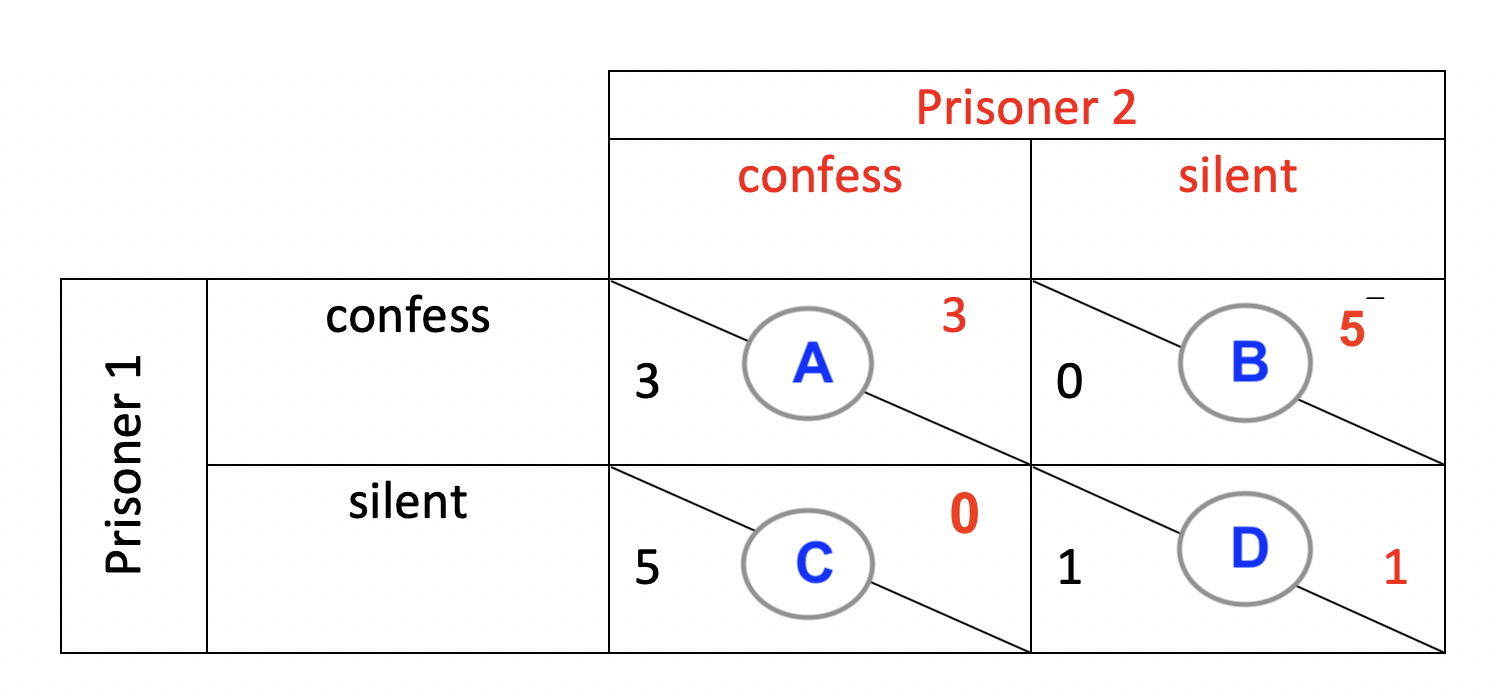
- Explain Nash equilibrium using payoff matrix from Prisoners' dilemma scenario.
- Your explanation should include examining the four outcomes, A, B, C & C as shown below and why some outcomes are not Nash Equilibrium and one is.
Badge It Platinum
- Conduct some research online and write 200 words on:
- What dominant strategy is
- Find an example of dominant strategy explain how the dominant strategy works in your example.