3.3.7 Representing Sound

• A sound is literally a vibration that travels through a medium (air) in waves by changing the air pressure as it moves.
• These waves hit our ear drums and our brains convert these into sounds that we can hear and understand.
• The compression and rareification of air can be represented graphically as shown below.

• The image from the oscilloscope shows a sound wave with varying amplitudes and frequencies.
• If we were to look at the y values, then we would see that the sound wave is fundamentally analogue in nature.

• Sound waves are analogue, which means continuously changing. Anything stored on a computer has to be stored in a digital format as a series of binary numbers 0's and 1's with nothing in between.
• In order to store sound in a digital format, there are a few steps that need to be followed:
  1. The Analogue sound must first be captured with an input device (Microphone).
  2. This sound is then converted to an electrical analogue signal.
  3. The signal amplitude (Height of the wave) is measured ar regular intervals (Sampled).
  4. The digital data is then rounded to a level (Quantisation).
  5. The digital data can then be stored as a series of binary numbers.

• Sampling is the process of converting an analogue sound wave into a digital format, and is a measure of amplitude.
• The accuracy with which an analogue sound wave is converted to a digital format depends on two things, Sample Resolution and Sample rate.
• Sample Resolution is the number of bits used to store each sample. This is sometimes also referred to as Bit Depth.
• The process involves recording the amplitude of an electrical signal at set intervals, rounding the value (Quantisation) and converting it to binary (typically 16 or 32 bits for sound).
• Sampling Rate is the frequency with which you record the amplitude of the sound, i.e. the number of samples per second. This is usually measured in Hertz (Hz). 1 Hz means one sample per second. 1 MHz (Megahertz) means one million times per second.
• The more frequently the sound is sampled, the better the quality and smoother the playback will sound.
• For sound, this sampling normally occurs 44,100 times per second. We call this the Sample Resolution and it is normally expressed as 44.1kHz.
• Obviously, the higher the Sample Rate and the larger the bit depth, the higher the quality of the resulting audio.

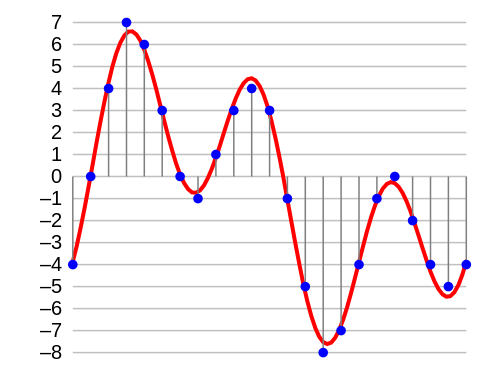
• The image above is a graphical representation of how an analogue electrical signal can be sampled and converted to an integer, ready for storing as a binary integer.

- Sample Rate (Frequency) - The number of samples per second.
- Sample Resolution - The number of bits used to store each sample.
- Seconds - The length in seconds of the whole sound file.
- The file size of a sample in bits = sample rate x sample resolution x number
  of seconds.
- The file size of a sample in bytes = sample rate x sample resolution x number
  of seconds / 8.

For Example

• Bit Rate (amount of Bits per second) = Sampling Rate * Sampling Resolution.
• CD has a sample rate of 44,100Hz, a Resolution of 16 bits.
• A sample rate of 44.1Hz is typically used for CD audio, with a sample resolution of 16 bits per sample.
• Bit Rate = 44,100 * 16 (bits) = 705,600bps / 1,000 = 705.6Kbps(Kilobits per second).
• File Size can then be calculated using the Bit Rate and length of the audio (seconds).
• CD has a Bit Rate of 705.6Kbps and has one song which is 3 minutes long:
  • File Size = 705.6Kbps * 180 seconds (3 * 60) = 127008Kb(Kilobits) / 1000 (Mega) / 8 (Bytes) = 15.88MB