Fundamentals of data structures- Tree
Table of Contents
1 Abstract data type - Tree
Tree Basics
A treeis an abstract data type that consists of a finite number of connected nodes.A treecan be thought as a undirected graph without cycles.- A tree can have or not have a
root node. A rooted tree has a root node at the top. - A tree has the following terms to describe it:
node: the node containing the tree dataroot node: the top node where there is no nodes from above it connecting to it.branch/edge/link: connection between nodes. Each node has exactly one edge/link from above it.child/child node: a set of nodes who have the same parent above them.parent: a node has child nodes below it.leaf node: a node that does not have any children.subtree: a substructure consisting a parent and all its descendants. A leaf node may also be a subtree.
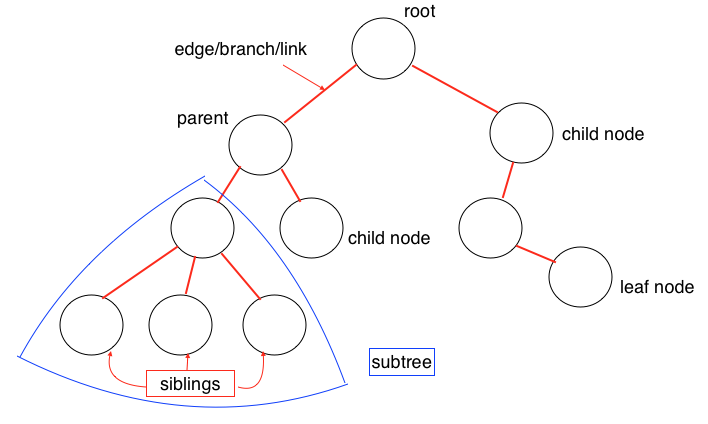
Binary Tree
A binary treeis a rooted tree structure where each node has a maximum twochild nodes.An example of a binary tree:
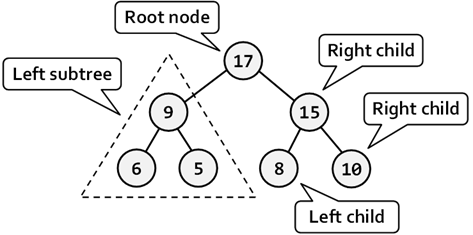
Creating a binary tree for search purpose - BST (Binary Search Tree)
- Starting with an array of data which may contain the search value:
4,7,3,44,5,6,9,44,36
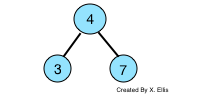
- Placing the first element, 4 as the root node
- Moving to the second element, 7. Comparing it with 4, if it is larger than it, place 7 to the right of 4.
- Moving to the third element, 3. Comparing with 4, placing it to the left of 4 since 3<4.
- Applying the above steps to place the remaining elements. Each time comparing the value to the root, then its child nodes.
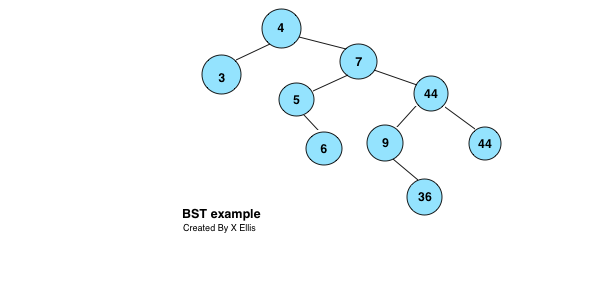
- When an equal value is encountered, such as 44, placing it to the right or left as long as the choice is consistent through out the tree constructing.
Exercise 1 (using the above BST example)
Question 1:
- List all the nodes visited when searching for the value 9
Question 2:
- Find the parent node for a new value 60
Question 3:
- What is the potential impact on search time from a not well balanced tree like the example?
2 Implementing a BST
Using an array of records
- Each node has three attributes:
- data
- left pointer
- right pointer
- Each record containing the above three attributes/fields for each node
- An array is used to hold all nodes.
Using three arrays or lists
- Each node has three attributes:
- data
- left pointer
- right pointer
- Each array/list holds one of the attributes for all nodes. One array/list for the left pointers, one array/list for the left pointers, and one array/list for the data items.
- Using our example BST data: 4,7,3,44,5,6,9,44,36, the arrays/lists will be:
array index arrayLeft dataArray arrayRight 0 2 4 1 1 4 7 3 2 -1 3 -1 3 6 44 7 4 -1 5 5 5 -1 6 -1 6 -1 9 8 7 -1 44 -1 8 -1 36 -1 - The value -1 is a rogue value to indicate a node without left or right child node.
3 Traversing A Binary Tree
Tree traversal (also known as tree search) is a form of graph traversal and refers to the process of visiting each node in a tree data structure, exactly once.
Classified by the order in which the nodes are visited, there are three ways to traverse a binary tree:
- Pre-order traversal
- In-order traversal
- Post-order traversal
Pre-order traversal
- Starting from the left side of the root node, going through the outline of the tree
- When passing the left of a node, access the value of that node
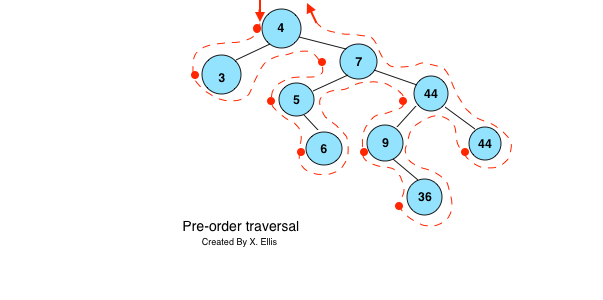
- The above BST pre-order traversal will produce the following sequence of data:
4, 3, 7, 5, 6, 44, 9, 36, 44
- Pre-order traversal can be used for making a prefix expression (Polish notation)
In-order traversal
- Starting from the left side of the root node, going through the outline of the tree
- When passing underneath a node, access the value of that node
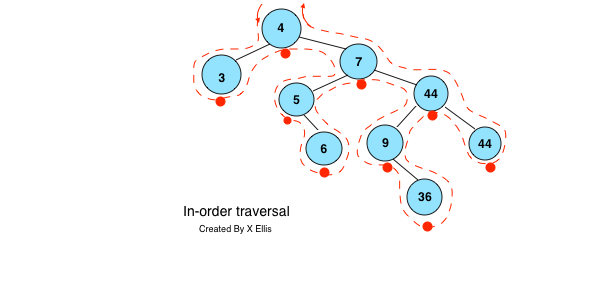
- The above BST pre-order traversal will produce the following sequence of data:
3, 4, 5, 6, 7, 9, 36, 44, 44
- In-order traversal can be used for returning a set of ordered values of a binary tree.
Post-order traversal
- Starting from the left side of the root node, going through the outline of the tree
- When passing the right side of a node, access the value of that node
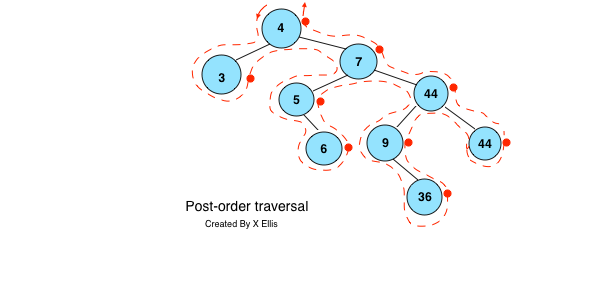
- The above BST pre-order traversal will produce the following sequence of data:
3, 6, 5, 36, 9, 44, 44, 7, 4
- Post-order traversal can be used during compilation to produce reserver polish notation.