Fundamentals of data structures- Graph

• Graphs are data strcutures that consist of a finite number of vertices/nodes/points and edges/arcs/lines connecting those vertices/nodes/points.
• Graphs can be undirected, directed and weighted.
• The edges/arcs/lines between nodes can be used to represent complex relationships.
  • Arrows on edges/arcs/lines can be used for directional relationships.
    • If edges on a graph are all one-way, the graph is a directed graph or digraph.
  • Attributes/values can be associated with edges/arcs/lines to specify the nature of relationships. Those edges with values are weighted edges.

An example of undirected graph:

An example of directed graph/digraph:

An example of directed graph with weighted edges:

• finite state machine
• roads between towns and cities with distances as weights
• computer networks: computers and devices as nodes and bandwidth as weights.
• Website: the vertices represent web pages and directed edges represent links from one page to another.
• In chemistry a graph makes a natural model for a molecule, where vertices represent atoms and edges bonds.
• In biology and conservation efforts where a vertex can represent regions where certain species exist (or inhabit) and the edges represent migration paths, or movement between the regions.

• Adding a node
• Deleting a node
• Adding an edge
• Deleting an edge
• Checking if there is an edge between node A and B
• Finding the successors of a given vertex
• Finding a path between two vertices

• Adjacency matrix:
  • Using a two-dimensional array, a weighted or unweighted graph can be implemented.

    

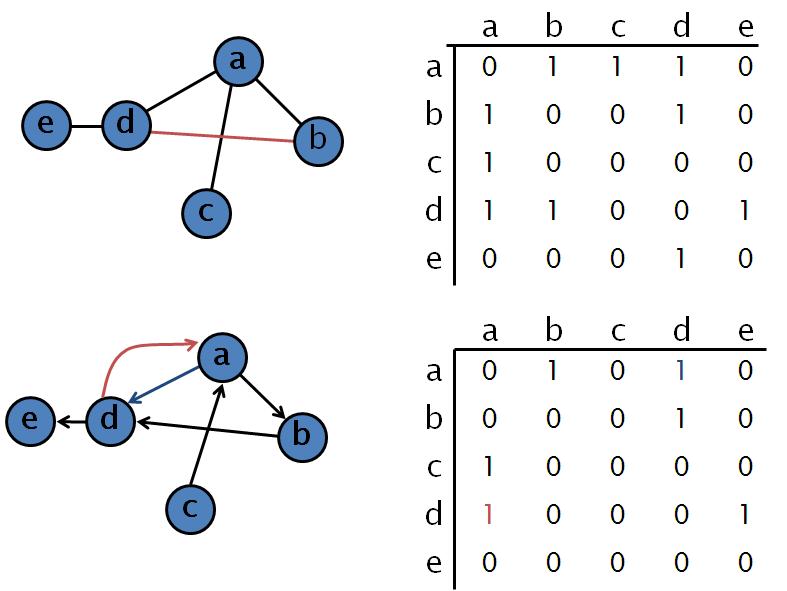
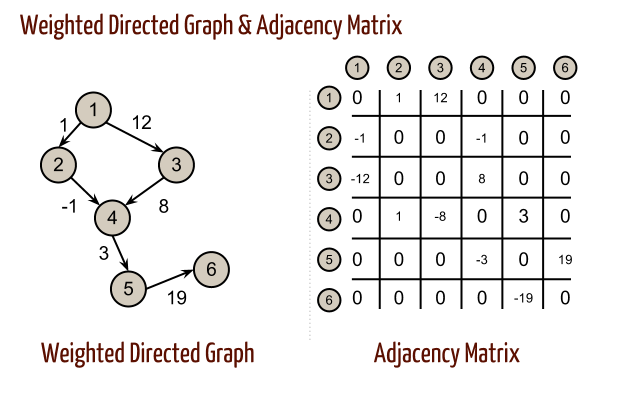
  • Advantages of adjacency matrix:
    • easy to add or remove an edge
    • easy to check if an edge existing
  • Disadvantages of adjacency matrix:
    • The larger the graph (more nodes), the more memory is needed.
    • For a sparse graph, space will be wasted for not storing many edges.
    • If static array is used for the matrix, adding or deleting nodes may not be easy.
• Adjacency list:
  • For a sparsely connected graph, adjacency list implementation is more space efficient. In this implementation:
    • All nodes are stored in a list
    • Each node in the list then points to a list of adjacent nodes it connects directly.
    • the adjacent node lists can contain a list of key value pairs of node and the weight.

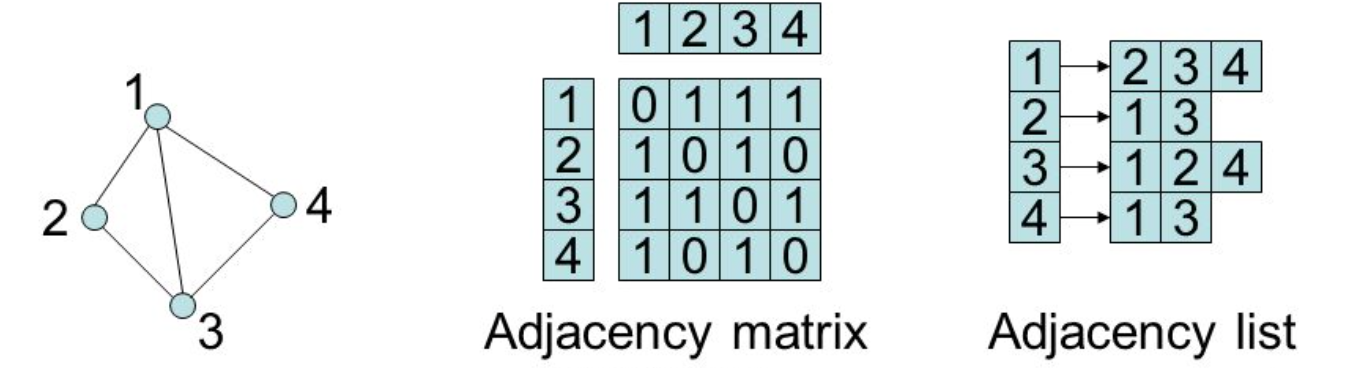
• Advantages of adjacency list:
  • Easy to find successors of a node
  • Easy to find all neighbouring nodes
  • Space efficient as it only stores connected nodes
• Disadvantage of adjacency list:
  • It is time consuming to check if an edge is part of a graph