Fundamentals of data structures

• Data structure is a collection of data that organised for easy processing.
  • Dynamic data structure is a collection of data in memory that can grow or shrink in size. Example: Python's list.
  • Heap is memory allocated at run-time for new items to dynamic data structure;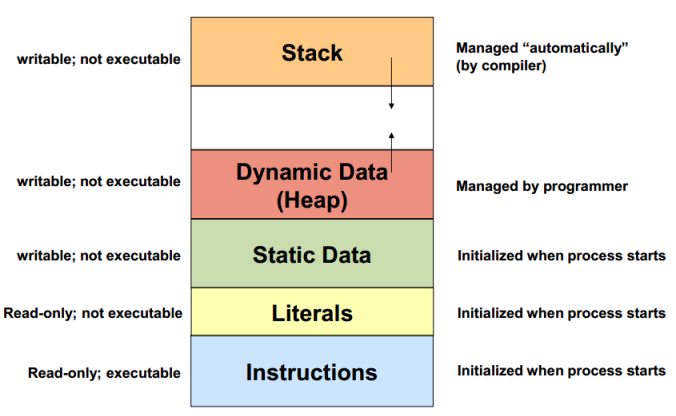
  • Static data structure is fixed in size at compilation time and cannot be resized to hold more items or to remove items to free up memory. Example: a static array in VB. Python does not have a built-in array type.
• Dynamic vs static data structure
  • Size of static structure fixed at compile-time whereas size of dynamic structure can change at run-time;
  • Static structures can waste storage space/memory if the number of data items stored is small relative to the size of the structure whereas dynamic structures only take up the amount of storage space required for the actual data.
  • Dynamic data structure is normally implemented using pointers which require extra memory space.
  • Data insertion with dynamic data structure involves adjusting pointers while static data structure requires moving data items which can be more complex.

• Array is a collection of elements with the same data type.
• One dimensional array has a single index to indicate the location/order of an item in the structure.
• Two dimensional array has two indices to indicate the location/order of an item in the structure such as a matrix, or a grid.
• Three dimensional array has three indices, such as points in a cube.

Objectives:

• Be able to read/write from/to a text file.
• Be able to read/write data from/to a binary (non- text) file.

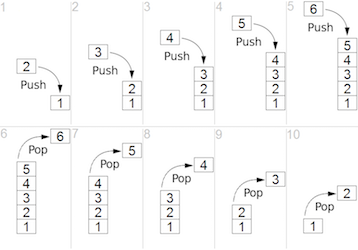
• Stack is an abstract data type with a collection of elements where a new element is added to the top of the stack (push) and the most recently added element is removed (pop) first.

By Maxtremus - Own work, CC0

• A stack has following operations performed on it:
  • push: add a new item to the top of the stack
  • pop: remove the most recently added element from the top of the stack
  • peek or top: read the content of the top element without modifying it
  • isFull: check if the stack is full
  • isEmpty: check if the stack is empty
• Pseudo-code for stack in OOP:

Stack = Class
   Private maxSize
   Public topOfStackPointer
   Public Procedure CreateStack
   Function push
   Function peek
   Function pop
   Function isEmpty

End

• The class entity diagram for the above:

• A queue is a first in first out (FIFO) data structure.
• New element is added to the end of the queue.
• Elements can only be retrieved from the start of the queue
• The order of the elements are the order in which they are inserted.
• Queues can be implemented using Array, Linked-list, Pointer.
• Queues can be used for:
  • printing: jobs to be printed is stored on disk in a queue. The printer prints them in the order it receives - first come first print. This allows users to work on other tasks after sending the printing jobs to the queue.
  • Keyboard buffer queue: characters stored in a queue in a keyboard buffer.
• Regardless what is used to implement a queue, the operations are the same.
• operations on queues:
  • add a new item to the end of the queue (enQueue())
  • retrieve the item at the start of the queue (peek)
  • remove an item from the start of the queue (deQueue())
  • check if a queue is empty (isEmpty())
  • check if a fixed size queue is full (isFull())
• A linear queue is one way of implementing a queue data structure using array.
  • New element added to the end.
  • When removing an item from the start, all other elements move up one position.
    • If the queue is very long, re-orgainising/re-positioning each element can take a long time.
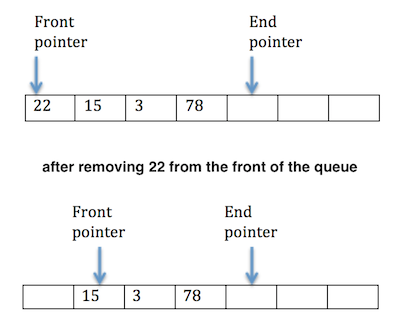
• A another way to implememt a linear queue is to use pointers:
  • The size of the queue is known
  • The current number of elements is known
  • One pointer is used to always point to the first element from the start of the queue
  • The other pointer is used to always point to the last element at the end of the queue
  • When an element is dequeued, the pointer points to the next element, resulting an empty space that cannot be used at the front.

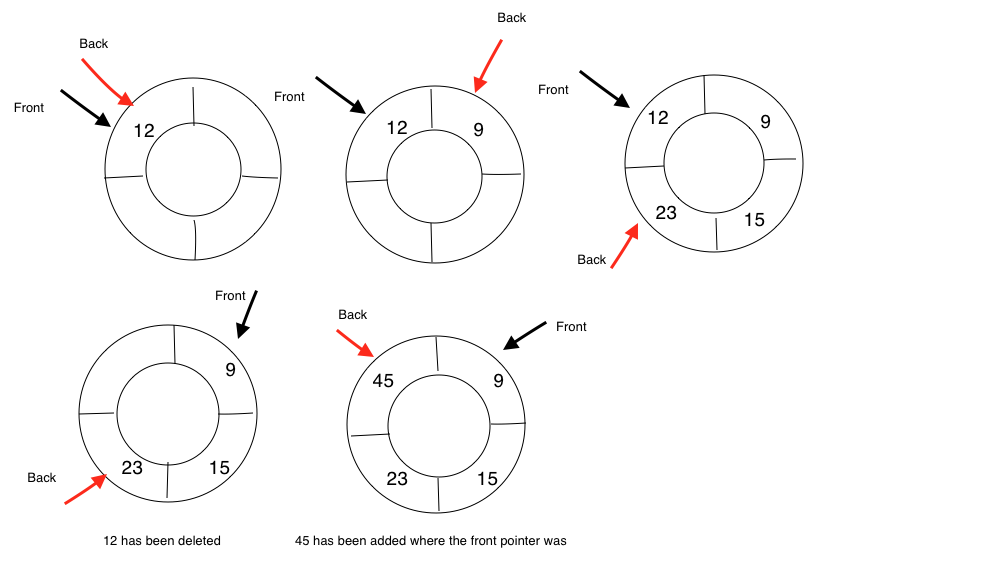
• A circular queue is a queue when the end pointer has reached the last element, when new item is added, it points to the start of the queue, thus forms a circle.
  • One pointer points to the first element
  • The other pointer points to the last element at the end of the queue
  • Add an element to the end of the queue and move the end pointer along
  • Remove element from the front of the queue and move the pointer to the next element at the front
  • After some deleting/removing operations, all available spaces are at the front of the queue,the end pointer will point to the starting position of the queue,thus forming a circular queue.

• Priority queue is a queue data structure where additionally each element has a priority associated with it. In a priority queue, an element with high priority is always removed before an element with low priority.
• Priority queue can be used by OS's scheduling program where certain system processes are given a higher priority than user processes.For example, an runtime error such as divid by zero, read/write file not found.

• A list is a collection of ordered elements of different data types,in contrast to array where all elements are of the same data type.
• A linked list is a list with each element/node/link contains a piece of data and a pointer (next pointer) pointing to the next element. A linked list has a head pointer that points to the first element and the last element's next pointer pointing to NULL.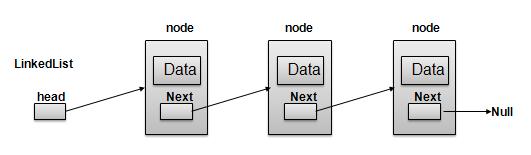
• The basic operartions of a linked list:
  • Insertion − Adds an element at the beginning of the list.

  

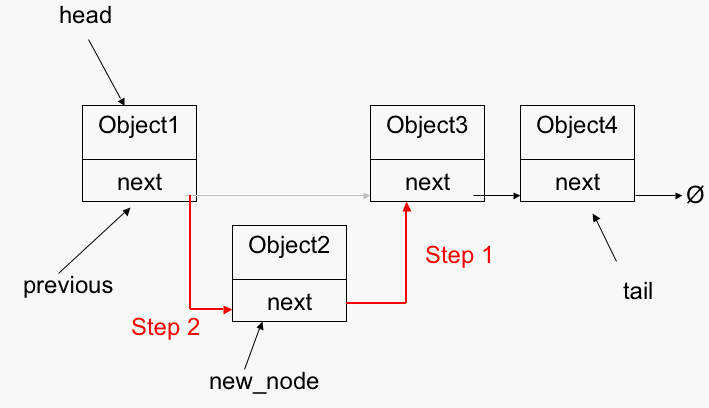
  • Deletion − Deletes an element from the list.

  

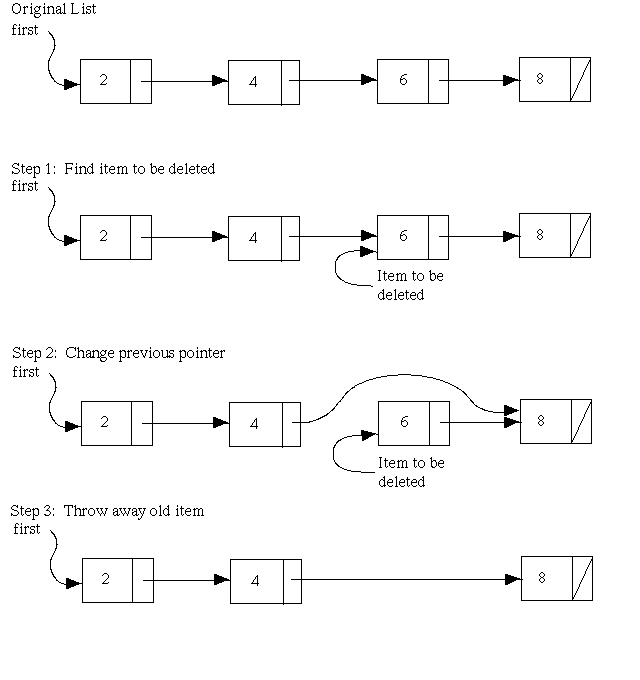
  • Display − Displays the complete list.
  • Search − Searches an element using the given key.

Click on the title to go to the separate page for content on graph.

Click on the title to go to the separate page for content on tree.

• Hash table is a data structure that maps keys to values. A hash function uses a key as the input to compute an index/location to an array of buckets, from which the desired value can be placed or found.
• The hash function narrows down the search record's location. Hash table allows data to be located quickly since the location of a record can be computed directly from the hash function.
• Hashing is used in database to make adding, deleting and searching records efficiently.

  

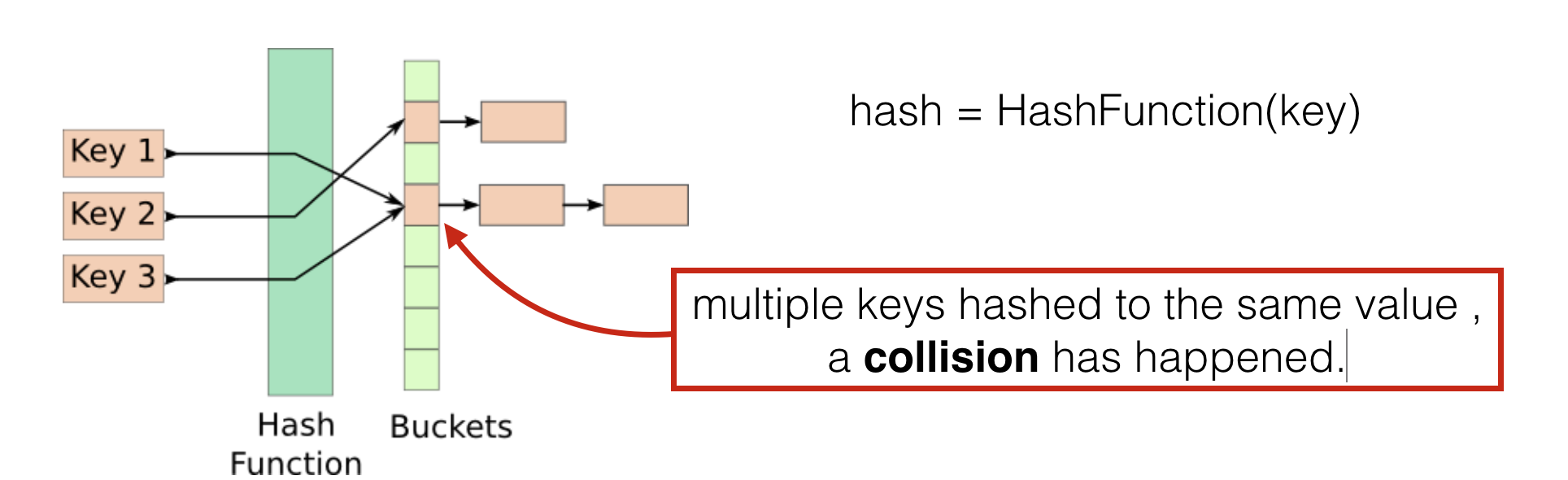
• A collision happens when two or more keys are hashed to the same hash values. There are different ways to deal with this when a collision happens.
• An example of hash function could be to add the ASCII denary values of characters for the key, then perform a modulo over the size of array.
• A perfect hash function will produce unique hashes for all available keys.
• Collision Resolution
  • if no collision resolution, when collision happens, the record or data can be overwritten.
  • one way to resolve collison is to find the next available space/location.
  • another way to resolve collision is to store a pointer at the location that is hashed to, and this pointer points to a list of all items that have the same hash values.
• Re-hash
  • to avoid more collisions happen, a new hash algorithm is needed
  • a larger hash table is also needed
  • all existing items' keys are re-hashed to the new, expanded table
  • all new data items will use this new hash algorithm to be inserted into the new, expanded table.

• A dictionary is an abstract data type(ADT) composed of a collection of (key, value) pairs, such that each possible key appears at most once in the collection.
• A dictionary not only can have a list of a single key to a single value, like this: {"Nathan":78, "Paul":92, "Roger":100}, it can also has a list of key to another list of values like this: {"Nathan":(56, 75,98), "Paul":(78, 79, 91)}, where the list could be first, second and third test marks for each name.
• operations on a dictionary may include:
  • extract all keys or values
  • check if certain key exists
  • get value for a given key
  • add, delete, modify (key, value) pair

• A set is a list of unsorted, unique values.
• A set is express as: S={a, ab, c}, T={c, d}
• A proper subset of a set A is a subset of A that is not equal to A. In other words, if B is a proper subset of A, then all elements of B are in A but A contains at least one element that is not in B.
  • For example: set A={a,b}, set B={a,b} and set C={a,b,c}
  • set A is not a proper subset of B, but both A and B are proper subsets of C.
• operations on a set:
  • union(S,T): returns the union of sets S and T.
  • intersection(S,T): returns the intersection of sets S and T.
  • difference(S,T): returns the difference of sets S and T.
  • subset(S,T): a predicate that tests whether the set S is a subset of set T.
• the Cartesian product A × B is the set of all ordered pairs (a, b) where a ∈ A and b ∈ B.

  For example:
  
      A = {1,2}; B = {3,4}
  
          A × B = {1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}
          B × A = {3,4} × {1,2} = {(3,1), (3,2), (4,1), (4,2)}
  

• Cardinality of a set is a measure of the "number of elements of the set". For example, the set A = {a, b, cd} contains 3 elements, and therefore A has a cardinality of 3.

Click the above link for the content on vectors.