Fundamentals of Functional Programming
Table of Contents
- 1. The Four Progamming Paradigms
- 2. Functional Programming Basics
- 3. Functional Programming Features
- 4. Function Application and Partial Function Application
- 5. First Class Object, Higher order functions
- 6. list Data Structure in Functional Programming
- 7. Define Functions
- 8. The three high order functions in list operations
- 9. Function Composition
1 The Four Progamming Paradigms
Imperative
Programming paradigmis a style of computer programming - different style approaching problems in different ways.- There are 4 major paradigms:
Procedural/imperative: a series of instructions that tell computers what to do with the input to solve a given problem. Eacg instruction changes the state of the operation, for example, change the value of variables.Object Oriented(OO): objects are used to model entities in solving a problem.Declarative: each statement describes the problem to be solved. Such as SQLFunctional: functions are used as the fundamental building blocks of a program. A series of functions accepting inputs are written to solve the given problem.
2 Functional Programming Basics
function
- a function,
f, has a function type - for a function f: A → B
- the function type is A → B
- A is the argument type
- B is the result type
- A function
type declarationcan be expressed in this form:
f:: Intger—>Integer add:: integer → (integer → integer) — add function takes two integers as arguments and gives an integer as a result.
- The set of inputs is called
domain - The set of possible outputs is called
co-domain. - For example: a function is defined as: f: A—>B where f(x) = x2
- The above function can be said the input in
domain Aproduces output inco-domain B - The domain and co-domain are always subsets of objects in some data type, for example, A: a set of real, B: a set of position real
- A function can also in the following form:
f: {Ed, Alex, Dan, Tom} —> {1122, 3452, 1234, 7892}
Ed maps to 1122, Alex maps to 3452 etc
The domain and co-domain can be of different data types
3 Functional Programming Features
Stateless and Immutable
Stateless: a variable’s previous state is not trackedImmutable: variable values cannot change- you cannot perform this in functional programming:
a = 2 a = a + 4
- Contrast imperative style with functional style:

Easy to write bug free, correct code - No side effect,Referential transparency
No side effects: functions can only perform some calculation and return some results- no I/O operations, no global state changes, no database interactions. In multithreads, one thread's operations will not affect others. The order of function calls will not affect the results.Referential transparency: same parameters will result in the same results regardless how many times the functions are called.- Easy to write bug free, correct code due to all the reasons above.
4 Function Application and Partial Function Application
Learn It
- The process of giving particular inputs to a function is called
function application, for example add(3,4) represents the application of the function add to integer arguments 3 and 4. Partial function applicationrefers to the process of fixing a number of arguments to a function, producing another function of smaller number of argumentsPartial function applicationin effect applying the function to produce new function that produce part of the computation:- if you fix the first arguments of the function, you get a function of the remaining arguments, for example, the function f below:
f: (x*y)—>W becomes partial(f) * y—>W Partial application gives a function partial(f), this function then applied to the second argument y.
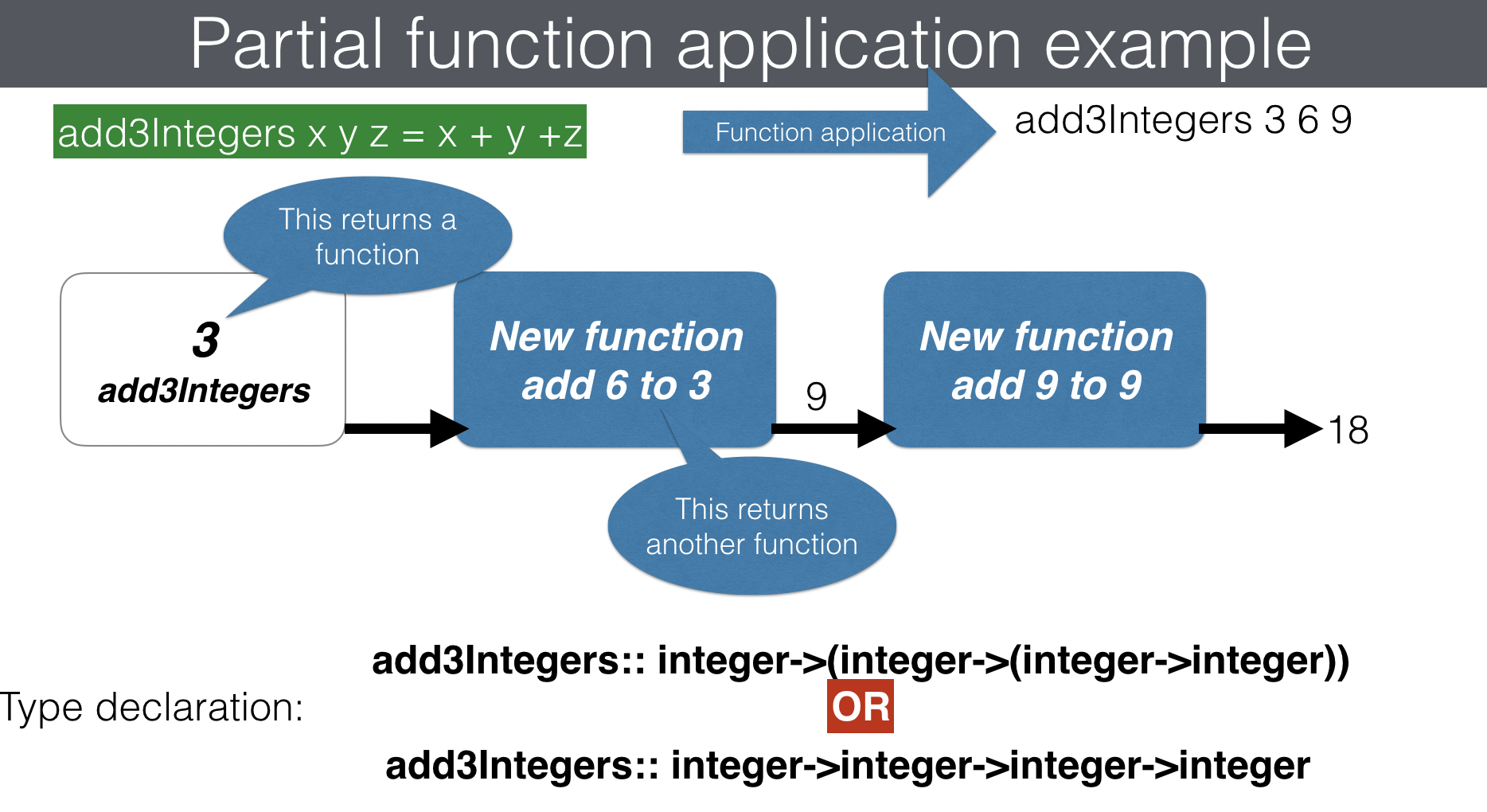
THINGS we learned from the above diagram:
- the function add3Integers has three integers as input and output another integer
- it actually only take one input at a time, for instance, the first input 3. This in turn produces a new function:
(integer->(integer->integer))
- the above new function then only takes one input 6. This in turn produces another new function:
(integer->integer)
- the above new function also only takes on input 9. This finally produces the resulting integer.
Partial Function Application Examples
- Consider the function add3Integers again:
type declaration: add3Integers:: integer->integer->integer->integer function definition: add3Integers x y z = x + y + z function application: add3Integers 3 6 9 partial function application: add3Integers 3 assign this to a new name: addTen = add3Integers 10 Therefore, this partial application allows for a fixed input 10 To apply the function addTen: addTen 6 9 The add3Integers applies to 6 then 9, then 10 to reach the final results.
- Haskell functions only take one argument/input at a time.
5 First Class Object, Higher order functions
First Class Object
First-class objects(or values) are objects which may:- appear in expressions
- be assigned to a variable
- be assigned as arguments
- be returned in function calls
- For example, integers, floating-point values, characters and strings are first class objects in many programming languages.
- When a function is a first-class object, it means it can be an argument to a function or a result of a function call
Higher-order functions
- A function is
higher-orderif it does at least one of the following:- takes a function as an argument
- returns a function as a result

6 list Data Structure in Functional Programming
Learn It: list and its common operations
- A list is a collection of items of similar type
in Haskel, list can be defined: >>>let studentList1= [“Tom”,”Ed”,”Alex","Dan","Dom"] >>>let studentList2 = [“Seamus","Adam","Ollie","Julian"] >>>let ids = [123,456,678,124,543,888]
- You can also define an empty list or add elements to an existing list:
Define an empty list >>> let myList = [ ] Test if an list is empty >>> null myList Append to a list (add more elements to the end) >>> studentList1 ++ [“Harry”] Preppend to a list (add more elements to the front) >>>[“Harry”, “Felix”] ++ studentList1
- List operations:
| function | usage | output | Note |
|---|---|---|---|
| head | head(studentLst1) | "Tom" | returns a single item |
| tail | tail(studentList1) | [”Ed”,”Alex","Dan","Dom"] | returns a list without the head |
| last | last(studentList1) | "Dom" | returns a single item |
| init | init(studentList1) | [“Tom”,”Ed”,”Alex","Dan"] | returns a list |
Check your understanding:
myList=["cat","dog","zebra","merekat"]
-
head(myList) returns
cat -
tail(myList) returns
["dog","zebra","merekat"] -
head(tail(myList)) returns
dog
7 Define Functions
Learn It
- To define a function, you can simply specify its name followed by the number of arguments and the function operations:
a function take an integer and times it by 2 doubleUp::Integer->Integer The type declaration doubleUp x = 2 * x The function definition doubleUp::Double->Double The type declaration has changed doubleUp x = 2 * x The function definition is the same
- To define a function takes a list as argument:
map f [] = [] Empty list input, empty list output map f (x:xs) = f x : map f xs
takeFirst:: [Integer]->Integer The function takes a list of integers takeFirst [] = Error "No data give" some useful error message if list is empty takeFirst xs = xs !! 0 Get the item from list xs at index 0
- another example:
average :: [Integer] -> Double average [] = error “No data given” average xs = fromIntegral(sum xs) / fromIntegral (length xs)
8 The three high order functions in list operations
Learn It: map function
mapis a high order function that takesa function and a listand applies that function to every element in the list, producinga new list.- Examples:
>>>map (+3) [4,5,2,9] [4, 8,5,12] >>> map (*6) [4, 5,2, 9] [24, 30, 12, 54] >>>map (max 4) [4, 5, 2, 9] [4, 5, 4, 9]
- An example with user defined function:
>>>DoubleUp x = 2 * x >>>myList = [4,5,2,9] >>>map DoubleUp myList [8,10,4,18]
Learn It: filter function
filteris a function that takes a a function that tells whether something is true or not, and a list and then returns the list of elements that returns true when applied the function.- function declaration: (a->Bool)->[a]->[a] - returns a list(the last argument) from all member of a list (the second argumen) meeting the condition set by the first argument.
- Exmaples:
>>> filter (>0) [-9, 8, 9, 2] [8,9,2] >>> filter (== 5)[-9, 5, 25, 12] [5] >>> filter even [-9,5,25,12] [12]
Learn It: reduce or fold function
reduce or foldfunction takes a list and reduces it to a single value by applying a function recursively to the list until the list is empty: apply the function to the head and recursively apply the function to the tail of the list.foldl: fold left function
foldl (-) 8 [10,20,30] Operationally, this is equivalent to: ((8-10) -20)-30 foldl (/) 10 [3,18,30] It is equivalent to:((10/3)/18)/30
foldr: fold right function
foldr (-) 8 [10,20,30] Operationally, this is equivalent to: (10-(20-(30-8))) foldr (/) 10 [3,18,30] It is equivalent to: 3/(18/(30/10))
- Use fold function to calculate factorial:
factorial n = foldr (*) 1 [1..n] [1..n] is an iterative expression of a list of numbers from 1 to n
Learn It: high order functions, list processing and recursion
- We touched recursion earlier in
foldfunction with list processing - The nature of recursiveness of applying function to a list is if a function can apply to the head of the list, then it should be able to apply to the rest of the list, the tail.
- Example 1:
reversefunction:- reverse (x:xs) = reverse xs +
- the (x:xs) notation is a way of expression a list with a head x and followed by its tail xs
- The above function applies the function
reverseto the head of the list , then recursive calls made to the tail of the list.
- Example 2:
takefunction- the take function takes n items from a list and return as a list
- it is defined as: take n (x:xs) = x : take (n-1) xs
- It applies the function
taketo the head of the list , then recursive calls made to the tail of the list.
- Example 3:
mapfunction- add2 x = x + 2, map add2 (x:xs) = add2 x : map add2 xs
- It applies add2 function to the head of the list , then recursive calls made to the tail of the list.
9 Function Composition
Learn It
functional composition: Combining two functions to get a new function.- For example, a function can be used as an argument in another function.
Given two functions: f: A—>B and g: B—>C The composition of g and f (g o f ) is a function. whose domain is A , co-domain is C Mathematically: f(x) = x + 5 and g(x) = 8x g o f = g(x+5) = 8(x+5) - the composition g of f
- Example 1:
notandevenare two separate functions- notEven is a composition
>>> notEven = not . even
- Example 2:
>>> squared x = x * x >>> addOne x = x + 1 >>> addOneSquared = squared . addOne >>> addOneSquared 2 9 >>>squaredAddOne = addOne . squared >>>squaredAddOne 2 5