AQA A NEA Evaluation Guideline
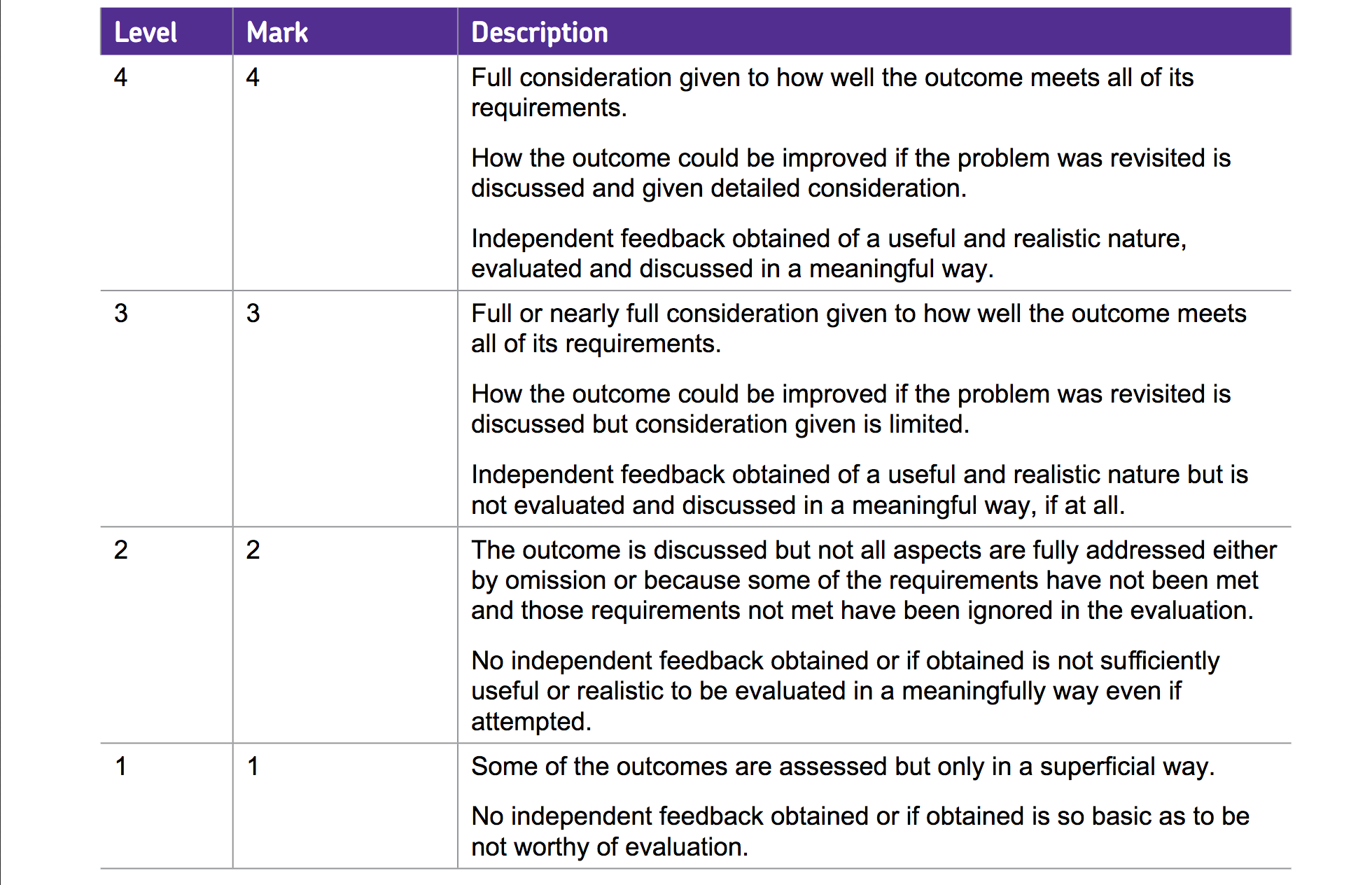
1 Expectations and Marking Scheme
Expectations
- see marking scheme below.
- always aim at the highest level.
- please pay attention to the independent feedback point and think about how you are going to obtain that, i.e. peer review? target users review?
When marking your work, I will be checking…
- have you given consideration as to how well the outcome meets the initial requirement?
- have you reflected on the objectives originally set and considered how their solution measures up to those objectives?
- have you obtained independent feedback and reflected upon this?
2 Present Your Evaluation
Structure
- Organise your write up in three sub-sections:
- evaluate aganist the requirements/objectives - how well the outcome meet the requirements. Referring back to the tests you have done that show you have met certain requirements/objectives.
- future improvement/different approaches if were to re-visit the same problem with reasons.
- detailed and realistic independent review/critique of the outcome. Get some feedback from your intended users. This can be a survey, interview summaries.
- A sensible approach would be to copy the objectives from the analysis into the evaluation so that each can be easily commented on. For each objective, the student could judge how effectively it has been met and also comment (if appropriate) on how the solution might be improved in this area.
- The student should aim to explain, in outline, how they might go about implementing the possible improvements. It is important that any third party feedback obtained is analysed by the students, not simply included as, for example, an email from the person.
- In addition to commenting on the individual objectives, students should also give an overview of the effectiveness of their solution, as it may be that some points would not be covered by commenting on the objectives alone. For example, some ideas for improving the system might be outside of the selected objectives.
- The actual feedback obtained from the third party should be included in an appendix. If feedback was also obtained at an earlier stage in the production of the project, for example based upon a prototype, then this could be referenced to in this evaluation so that it could be considered for credit.