How A Computer Works
1 Learning Objectives
By the end of the lesson…
- All Should Be able to apply Boolean logic to predict the output from a series of gates (half adder).
- All Should Be able to utilise a Full Adder to determine the binary addition of two numbers.
- Most Should Be able to simulate the Full Adder circuitry within Python.
- Some Could Be able to simulate and evaluate a binary subtractor within Python.
2 All the gates
Learn It
- In the last lesson we looked at how we can combine NAND gates to form other types of gates. Let's have a look at each of the gates and see how we can use them.
- You can click on the input buttons to see what each does.
- The first you should now be familiar with - The NAND gate.
- The next is the NOT gate, sometimes called an inverter.
- Then there is the AND gate
- This is an OR gate
- This is the opposite of an OR gate, called a NOR gate
- This last one is called an XOR gate
3 A bit of an adder
Learn It
- So what is the use of all these logic gates?
- Well combining all these logic gates together allows computers to actually work.
- A computer's main job is to store and process data.
- In the first lesson, you learned how to add binary numbers together. Computers use logic gates to do this. Let's start simply and just show the layout for adding two bits together.
Try It
- Try it out. The two inputs indicate the bits you want to add together.
- The upper output is the result of the addition, while the lower output is the carry.
0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 and carry 1 (so 10)
- This is called a Half Adder Circuit.
4 A bit more of an adder
Learn It
- A Full Adder can be constructed with XOR, AND and OR gates.
- The difference between a Full Adder and a Half Adder, is that the Full Adder has an additional input. This is where the carry from the previous calculation can be placed.
- Have a look at the circuit below.
Try It
- Let's have a go at a simple calculation. Say we want to add
111to11. - Let's align the two binary numbers.
111 11+ ---
- Starting from the right, we need to add the two ones together. So on the circuit, click the inputs A and B so that they are both 1s.
- We see the result is
0with a Carry of1 - Let's write that down.
111 11+ --- 0 --- 1
- Next we need to add the second column, but this now contains a Carry as well.
- Click buttons to make the inputs A and B set to
1, and also the input C as this represents the Carry from the previous calculation. - We see that we get a Result of
1with a Carry of1. - Let's write that down.
111 11+ --- 10 --- 11
- Our third column now contains a
1and the1carried over from the previous calculation. - Click the buttons to set A to
1and C to1 - We get a result of
0with a1Carry. - Let's write that in.
111 11+ --- 010 --- 111
- We now have a fourth column containing nothing but a Carry.
- If we set C to
1and A and B to0, we get a result of1, so we can write that in as well.
111 11+ --- 1010 --- 111
- And there we have a result
1010
5 Assessment
Badge It - Silver
- Demonstrate that you can use the full binary adder.
- Work in pairs. One of you should write down a binary addition to perform, and write down the results each time.
- The other member of the pair should operate the adder. You should be able to perform this without speaking.
- Ask your teacher to provide you with a binary addition to perform and demonstrate your skills.
- Here are some to practice on.
10 + 11,111 + 100,1010+1110
6 Abstraction
Learn It
- So what?
- Well let's just think back a little. All the Logic gates shown above can be constructed from NAND gates. And each NAND gate can be constructed from a couple of transistors.
- We've abstracted the circuits a little - which basically means we've simplified the rules without actually changing them. We could look at circuits containing dozens of transistors, but it would be difficult to work out what was going on. Redrawing transistor circuits using NAND gates is one layer of abstraction. Redrawing NAND gate circuits using AND, OR, XOR and NOR gates is another layer of abstraction.
- Let's remember that computer chips contain billions of transistors. What's more, the chips can flick those inputs and outputs billions of times a second. Imagine how quickly you could perform binary addition calculations if you could click the inputs and outputs of the Binary Adder a billion times a second. Imagine how quickly you could do it if you had a billion people sitting at a billion computers helping you out!
7 Abstracting with code
Learn It
- We can simulate logic gates in computer code.
- Create a new Python script using you're preferred text-editor or IDE (probably IDLE)
- Now copy and paste in this code.
def AND(A,B):
return A and B
def OR(A,B):
return A or B
def NOT(A):
return 1 - A
def NOR(A,B):
return 1-(A or B)
def NAND(A,B):
return 1 - (A and B)
def XOR(A,B):
return A ^ B
- Now run the script.
- Try typing the following into your interpreter -
AND(0,0) - How about the following -
AND(1,1),OR(1,1),NOR(1,1) - You should see that each of the functions is acting as a logic gate.
- We can store the output of any of the functions using a variable.
D = AND(1,0)for instance.- We can then pass that variable into another function.
- OR(D,1)
- The half-adder has only two gates: XOR and AND
- Here is the full script for the Half-adder
Try It
- Try running the script using different values for the inputA and inputB and check that it works the same as the circuit.
8 Assessment
Badge It - Gold
- To be awarded your Gold badge, you need to implement the Full Adder in code.
- Remember - you can pass the output from one function to another function.
- Look at the circuit, and use it to help you pass the outputs of one function to another.
D = AND(inputA,inputB) E = NOR(inputA,inputB) outputF = XOR(D,E)
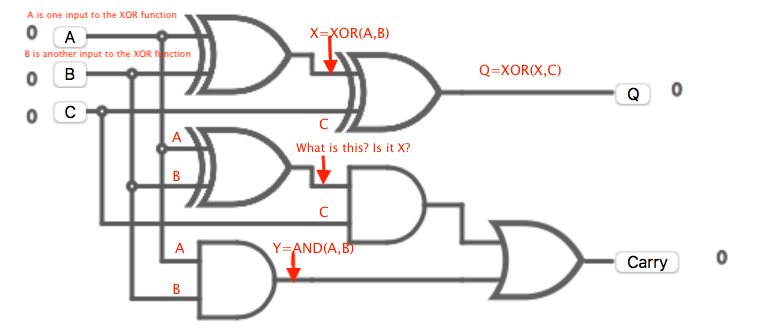
- The following is a partially finished/implemented full adder in Python.
- Try to finish the full adder in Python and test it by using the image above to help you.
- Upload your finished code to www.bournetolearn.com
9 Assessment
Badge It - Platinum
- Here is the circuit for a Full Subtractor from Wikipedia

- Use this circuit to construct a Full Subtractor in Python code. Demonstrate it to your teacher when you have finished it.